Definición
Sean dos vectores a y b en el espacio vectorial ?3. El producto vectorial entre a y b, como se mencionó antes, da como resultado un nuevo vector, al que llamaremos c. Para definir este nuevo vector es necesario especificar su módulo, dirección y sentido:- El módulo de c está dado por
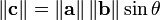
- La dirección de c es tal que c es ortogonal a a y ortogonal a b.
- El sentido en el que apunta el vector c está dado por la regla del sacacorchos.
El producto vectorial puede definirse de una manera más compacta de la siguiente manera:
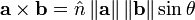 donde
donde 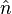 es e
es e
No hay comentarios:
Publicar un comentario