Funciones Parametricas
FUNCIONES EXPRESADAS EN FORMA PARAMETRICA
Una representación parametrica frecuentemente puede constituir la regla de correspondencia de una función .
Las ecuaciones x= cosq;y =2 senq,en las que q es el parámetro, corresponden a la elipse de la ecuación cartesiana.
x2/9 + y2/4 =1
desde luego en estas ecuaciones ecuaciones definen multiforme en el intervalo abierto –3< x <3,que puede descomponerse en las dos siguientes funciones:
f1=í(x,y)ï x= 3 cos q, y= 2sen q, -3< x < 3, y>0ý
f2=í(x,y) ê x= 3 cos q ,y= 2 senq ,-3 < x <3, y <0ý
Una aplicación útil de las representaciones parametricas se presenta en problemas de movimiento curvilíneo donde comúnmente se considera que (x,y)son las coordenadas cartesianas del punto “x”.
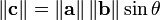
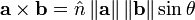 donde
donde 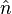 es e
es e