sábado, 20 de noviembre de 2010
viernes, 19 de noviembre de 2010
jueves, 18 de noviembre de 2010
lunes, 15 de noviembre de 2010
sábado, 13 de noviembre de 2010
viernes, 12 de noviembre de 2010
derivada direccional
En el análisis matemático, la derivada direccional de una función multivariable sobre un vector dado, representa la tasa de cambio (pendiente) de la función en la dirección de dicho vector. Este concepto generaliza a las derivadas parciales, ya que estas son derivadas direccionales en los vectores paralelos a los ejes.
lunes, 8 de noviembre de 2010
domingo, 7 de noviembre de 2010
regla de la cadena
En calcula, la regla de la cadena es una fórmula para la derivada de la composición de dos funciones. Tiene aplicaciones en el cálculo algebraico de derivadas cuando existe composición de funciones.
Descripción de la regla
En términos intuitivos, si una variable y, depende de una segunda variable u, que a la vez depende de una tercera variable x; entonces, la razón de cambio de y con respecto a x puede ser computado como el producto de la razón de cambio de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.
viernes, 5 de noviembre de 2010
viernes, 10 de septiembre de 2010
definicion
Funciones Parametricas
FUNCIONES EXPRESADAS EN FORMA PARAMETRICA
Una representación parametrica frecuentemente puede constituir la regla de correspondencia de una función .
Las ecuaciones x= cosq;y =2 senq,en las que q es el parámetro, corresponden a la elipse de la ecuación cartesiana.
x2/9 + y2/4 =1
desde luego en estas ecuaciones ecuaciones definen multiforme en el intervalo abierto –3< x <3,que puede descomponerse en las dos siguientes funciones:
f1=í(x,y)ï x= 3 cos q, y= 2sen q, -3< x < 3, y>0ý
f2=í(x,y) ê x= 3 cos q ,y= 2 senq ,-3 < x <3, y <0ý
Una aplicación útil de las representaciones parametricas se presenta en problemas de movimiento curvilíneo donde comúnmente se considera que (x,y)son las coordenadas cartesianas del punto “x”.
viernes, 3 de septiembre de 2010
definicion producto vectorial
Definición
Sean dos vectores a y b en el espacio vectorial ?3. El producto vectorial entre a y b, como se mencionó antes, da como resultado un nuevo vector, al que llamaremos c. Para definir este nuevo vector es necesario especificar su módulo, dirección y sentido:- El módulo de c está dado por
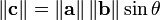
- La dirección de c es tal que c es ortogonal a a y ortogonal a b.
- El sentido en el que apunta el vector c está dado por la regla del sacacorchos.
El producto vectorial puede definirse de una manera más compacta de la siguiente manera:
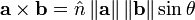 donde
donde 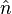 es e
es emiércoles, 1 de septiembre de 2010
viernes, 27 de agosto de 2010
viernes, 20 de agosto de 2010
Suscribirse a:
Comentarios (Atom)














.png)

